课上猜出答案，中午睡觉时突然就会了证明，记录一下。

题目大意：平面四边形 $ABCD$ 中 $|AB|=|AC|=|CD|=1,\angle ACD=\frac{\pi}{3},\angle CAB=\frac{\pi}{4}$ ，沿 $AC$ 翻折 $\triangle ACD$ 形成 $\triangle ACP$，求二面角 $A-CP-B$ 余弦最小值。

Key Observation 1:观察到转ACP和ABC是本质相同的

为什么选择转ABC：这是一个直角三角形，而且旋转定点不在交线上，这就意味着我需要刻画的的是点而非线，而且这甚至是个等腰直角三角形，性质非常优秀。

让我们画出示意图：

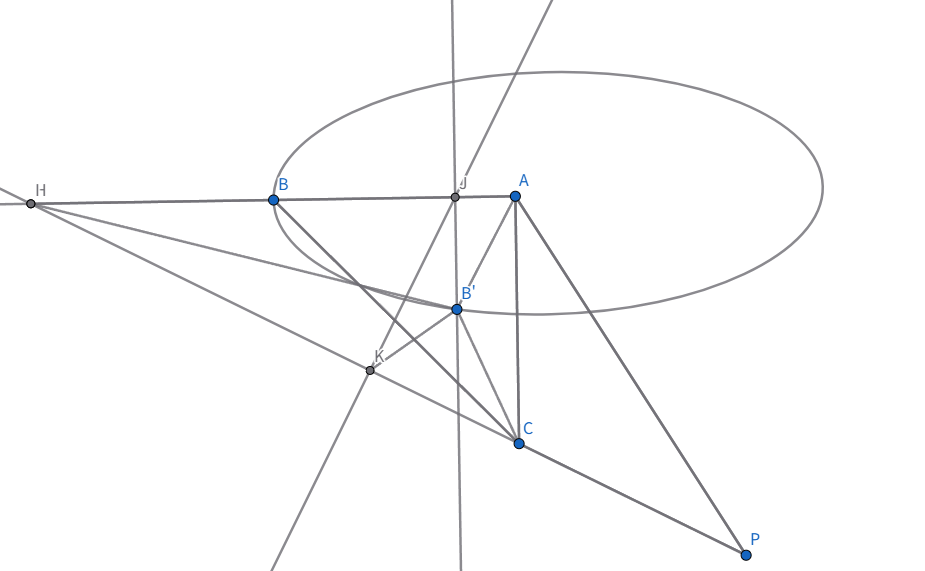
image.png

延长 $PC,BA$ 交于点 $H$。 上面的椭圆是 $B$ 点的轨迹。 $B’$ 是运动中的 $B$ 点， $J$ 是 $B’$ 在原平面的投影。 $JK \perp CP,B’K \perp CP$。 此时二面角等于 $\angle JKB’$。

Key Observation 2: $\triangle JB’H$ 和 $\triangle JB’K$ 是投影关系

这就意味着当 $\angle JKB’$ 最大时， $\angle JHB’$ 也是最大，而 $\angle JHB’$ 最大的时候就是相切。

接下来就是简单的带入计算了，计算得此时 $\cos \angle JKB’= \frac{\sqrt{3}}{3}$。